22 Hubs and Authorities
In Chapter 21 we saw a way to think of centrality as being “reflected” in the connections you have with others. Rather than being a property of the person, centrality is a property of the relations that a given person has with central others. We studied that idea in the case of an undirected graph, which gave us a conception of this type of reflective centrality as eigenvector centrality.
In this chapter we extend this idea to the case of asymmetric relations represented as a directed graph. The added complexity is that we have to think of two ways people’s centrality is reflected from their connections to others. On the one hand, a person can be central because many people seek their advice or services, or think of them as smart, capable, likable, and so on. That is, people are central when they receive many directed ties from other people. We will call these people authorities (Kleinberg 1999).
At the same time, there are people who while not being authorities themselves, serve as a conduit to authorities. These people get their centrality by pointing to authorities, and you get centrality by pointing to them (because that puts you just a few steps away from authorities). Thus a person who direct ties to many other people who are themselves authorities has a certain knowledge of the social structure that is valuable (they know the people who others need to know). We will call these people hubs (Kleinberg 1999).
At first pass, the distinction between hubs and authorities thus boils down to this:
Authorities are people who are pointed to by many other people.
Hubs are people who point to authorities.
Nevertheless, as we discussed in Chapter 23, not all people are created the same. A really good authority should be a person who gets lots of incoming nominations, not just from everyone, but from people who are also considered good hubs by other people. And what is a good hub? Well a good hub is a person who points to really good authorities. Thus, your status as an authority or a hub is both reflective and recursive. The reason for this is that the “goodness” of authorities and hubs is defined in terms of one another, just like the snake eating its own tail we found in Chapter 21.
Thus, if \(\mathbf{u}\) is a \(n \times 1\) column vector containing the authority scores of a set of nodes in a graph—a set of numbers ranking nodes from top to bottom in terms of their authoritativeness–and \(\mathbf{v}\) is a column vector of the same length containing the hub scores—a set of numbers ranking nodes from top to bottom depending of how good they are in pointing to authorities—then the two vectors \(\mathbf{u}\) and \(\mathbf{v}\) should be linked by the following mathematical relationship:
\[ \mathbf{u} = A^T \mathbf{v} \tag{22.1}\]
\[ \mathbf{v} = A \mathbf{u} \tag{22.2}\]
Where \(A\) is the adjacency matrix. That is, the authority scores should be a function of the hub scores of the incoming ties to a node—recorded in the transpose of the original adjacency matrix \(A^T\)—and the hub scores should be a function of authority scores of the outgoing ties to a node—recorded in the origina adjacency matrix \(A\).
Note that in Equation 22.1 and Equation 22.2 we face the same chicken and the egg problem we encountered in Chapter 21. Because the authorities scores are defined in terms of the hub scores, we can’t figure those out until we find the hub scores, but because the hub scores are defined in terms of the authority scores we can’t figure those out until we find the authority scores!
The solution to our dilemma is similar to the one we used in Chapter 21. We can give each node in the network the same number of “starting” hub points to give out to every node they point to for free—let’s say every node with an outgoing edge gives one hub point to their out-neighbor—and then calculate the authority scores of all nodes \(\mathbf{u}\) using Equation 22.1. Then we can use those \(\mathbf{u}\) scores to calculate the hub scores \(\mathbf{v}\) using Equation 22.2. A node’s authority score is the sum of the hub scores of the nodes that point to it, and a node’s hub score is the sum of the authority scores of the nodes they point to. We rinse, repeat and stop once the rank order of nodes on both the authority and hub ranking stops changing.
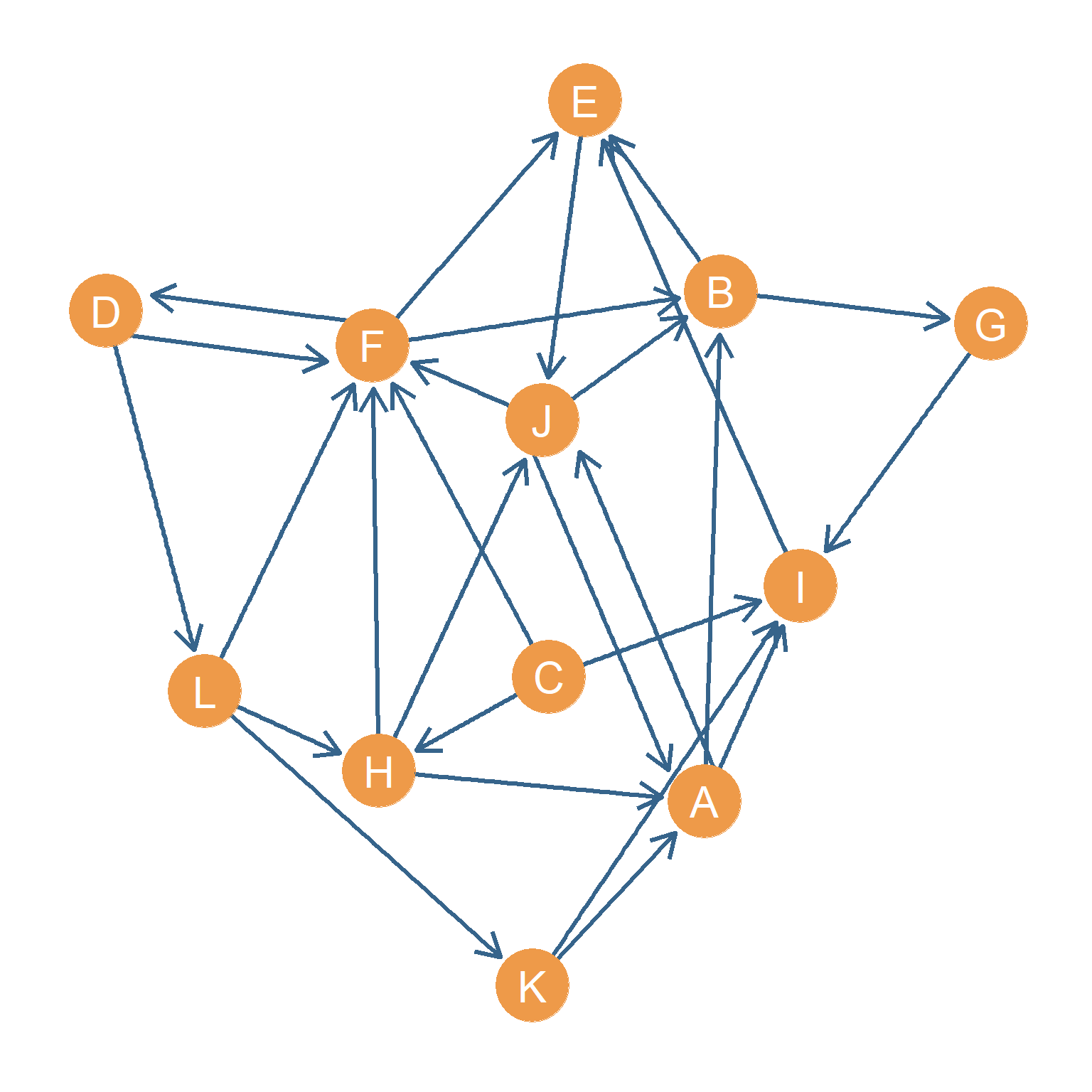
How would this work in a social network? Let us see. Figure 23.1 shows a directed graph representing a set of asymmetric ties between people (this is the same graph from Chapter 23) and Table 23.1 is the corresponding adjacency matrix.
| A | B | C | D | E | F | G | H | I | J | K | L | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| B | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| C | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| D | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| E | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| F | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| G | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| H | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| I | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| J | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| K | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| L | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
Table 22.1: Adjacency matrix corresponding to a directed graph.
Now, let’s assign everyone “one” hub point to begin with. That means that the the \(\mathbf{v_1}\) column vector that goes into Equation 22.1 will just be a \(12 \times 1\) column vector full of ones. This is shown in Table 22.2 (a)
Thus, when we plug the numbers in Table 22.2 (a) into Equation 22.1, we get a column vector with the entries shown in Table 22.2 (b). Note that these are the in-degrees of each node in the graph. This makes sense, because multiplying an adjacency matrix times the all ones vector results in a vector that is just the row sums of the original matrix (as we learned in Chapter 16).
Multiplying the transpose of the adjacency matrix times the all ones vector gives us the row sums of the transpose, which is the same as the column sums of the original adjacency matrix (which is how we calculate in-degree centrality; see Chapter 20).
Now all we need to do is plug the authority score vector \(\mathbf{u_1}\) shown in Table 22.2 (b) into Equation 22.2 to calculate the new hub score vector \(\mathbf{v_2}\) But before we do that we normalize the authority score vector \(\mathbf{u_1}\) by dividing by the maximum observed score (\(max(\mathbf{u_1}) = 5\), to get the new authority score vector \(\mathbf{u_1}\) shown in Table 22.2 (c). We plug in these entries into Equation 22.2 and divide by the maximum, to get the hub score vector \(\mathbf{v_2}\) shown in Table 22.2 (d).
Table 22.2: First four steps in finding hub and authority scores.
| A | 1 |
| B | 1 |
| C | 1 |
| D | 1 |
| E | 1 |
| F | 1 |
| G | 1 |
| H | 1 |
| I | 1 |
| J | 1 |
| K | 1 |
| L | 1 |
| A | 3 |
| B | 3 |
| C | 0 |
| D | 1 |
| E | 3 |
| F | 5 |
| G | 1 |
| H | 2 |
| I | 4 |
| J | 3 |
| K | 1 |
| L | 1 |
| A | 0.6 |
| B | 0.6 |
| C | 0.0 |
| D | 0.2 |
| E | 0.6 |
| F | 1.0 |
| G | 0.2 |
| H | 0.4 |
| I | 0.8 |
| J | 0.6 |
| K | 0.2 |
| L | 0.2 |
| A | 0.91 |
| B | 0.36 |
| C | 1.00 |
| D | 0.55 |
| E | 0.27 |
| F | 0.64 |
| G | 0.36 |
| H | 1.00 |
| I | 0.27 |
| J | 1.00 |
| K | 0.64 |
| L | 0.73 |
Of course, the point is to keep this iteration going until we have minimal differences between the \(\mathbf{u_k}\) and \(\mathbf{u_k}\) vectors at step \(k\) and those we found at step \(k - 1\). After 20 iterations, we find the final hub and authority scores shown in Table 22.3 (a) and Table 22.3 (b), which each node arranged from top to bottom according to their respective scores.
Table 22.3: Final hub and authority scores.
| F | 1.00 |
| I | 0.61 |
| A | 0.60 |
| B | 0.48 |
| J | 0.46 |
| H | 0.41 |
| K | 0.18 |
| L | 0.13 |
| E | 0.10 |
| D | 0.07 |
| G | 0.01 |
| C | 0.00 |
| J | 1.00 |
| H | 0.99 |
| C | 0.96 |
| L | 0.76 |
| A | 0.74 |
| K | 0.58 |
| D | 0.54 |
| F | 0.31 |
| G | 0.29 |
| E | 0.22 |
| B | 0.05 |
| I | 0.05 |
As we can see from Table 22.3 (a), node \(F\) is the undisputed authority in the network. If Figure 23.1 was an advice network, that’s the person you’d want to go to, because the people who other people go to, also go to them.
Nevertheless, if you didn’t know that \(F\) was the main authority, you’d want to ask the people who seek advice from that authority even if not that many people seek advice from them. These are the “hubs” in the network, and they happen to be nodes \(J\), \(H\), and \(C\).
Node \(C\) is an interesting case; no one points to \(C\) (\(C\)’s in-degree is zero which makes them last in the authority rank as shown in Table 22.3 (a)), but because \(C\) points to \(F\), it makes them one of the best hubs (so still a good person to know, because he knows who the important people are).
Now as you recall from Chapter 21, every time we have this kind of chicken and the egg, snake eating its own tail problem, it seems to also be possible to compute the rankings without iterating back and forth, and instead solving a matrix equation using linear algebra methods (Bonacich 1972). This time is no exception.
Consider the matrix \(B\) that results when we multiply the transpose of the adjacency matrix times the original adjacency matrix:
\[ B = A^TA \tag{22.3}\]
This matrix is shown in Table 22.4. As we have seen, this matrix records the number of common in-neighbors that the row node i has with the column node j (with the diagonals recording the in-degrees of each node).
| A | B | C | D | E | F | G | H | I | J | K | L | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 3 | 1 | 0 | 0 | 0 | 2 | 0 | 0 | 1 | 1 | 0 | 0 |
| B | 1 | 3 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| C | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| D | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| E | 0 | 1 | 0 | 1 | 3 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| F | 2 | 1 | 0 | 0 | 0 | 5 | 0 | 2 | 1 | 1 | 1 | 1 |
| G | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| H | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 2 | 1 | 0 | 1 | 0 |
| I | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 4 | 1 | 0 | 0 |
| J | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 3 | 0 | 0 |
| K | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| L | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
Now also consider the matrix \(C\) that results when we multiply the original adjacency matrix times its transpose:
\[ C = AA^T \tag{22.4}\]
This matrix is shown in Table 22.5. As we have also seen, this matrix records the number of common out-neighbors that the row node i has with the column node j (with the diagonals recording the out-degrees of each node).
| A | B | C | D | E | F | G | H | I | J | K | L | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 3 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 |
| B | 0 | 2 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| C | 1 | 0 | 3 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 2 |
| D | 0 | 0 | 1 | 2 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| E | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| F | 1 | 1 | 0 | 0 | 0 | 3 | 0 | 0 | 1 | 1 | 0 | 0 |
| G | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| H | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 3 | 0 | 2 | 1 | 1 |
| I | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| J | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 2 | 0 | 3 | 1 | 1 |
| K | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 2 | 0 |
| L | 0 | 0 | 2 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 3 |
It turns out that our final authority score vectors \(\mathbf{u}\) hub score vectors \(\mathbf{v}\) are equivalent to the ones that solve the following equations:
\[ B\mathbf{u} = \lambda^B \mathbf{u} \tag{22.5}\]
\[ C\mathbf{v} = \lambda^C \mathbf{v} \tag{22.6}\]
Which means that \(\mathbf{u}\) in Equation 22.5 is an eigenvector of the common in-neighbors matrix \(B\) and \(\mathbf{v}\) in Equation 22.6 is an eigenvector of the common out-neighbors matrix \(C\) (with \(\lambda^B\) and \(\lambda^C\) being the corresponding eigenvalues). In fact, \(\mathbf{u}\) and \(\mathbf{v}\) are the leading (first) eigenvectors of the common in and out-neighbors matrices (respectively). The absolute values of these two eigenvectors are shown in Table 22.6.
Table 22.6: Final hub and authority scores according to the eigenvalues of the in and out-neighbor matrices.
| F | 0.645 |
| I | 0.391 |
| A | 0.390 |
| B | 0.312 |
| J | 0.296 |
| H | 0.261 |
| K | 0.115 |
| L | 0.082 |
| E | 0.063 |
| D | 0.048 |
| G | 0.008 |
| C | 0.000 |
| J | 0.452 |
| H | 0.447 |
| C | 0.435 |
| L | 0.343 |
| A | 0.335 |
| K | 0.262 |
| D | 0.244 |
| F | 0.142 |
| G | 0.131 |
| E | 0.099 |
| B | 0.024 |
| I | 0.021 |
As we can see the order of nodes in terms of authority and hub scores is the same as that obtained by the iterative procedure!
References
Bonacich, Phillip. 1972. “Factoring and Weighting Approaches to Status Scores and Clique Identification.” Journal of Mathematical Sociology 2 (1): 113–20.
Kleinberg, Jon M. 1999. “Authoritative Sources in a Hyperlinked Environment.” Journal of the ACM (JACM) 46 (5): 604–32.